射频 - 谐振电路 - 基本定义

在这一大章节下，我们将研究并联谐振电路及其在射频下的特性，负载 Q 的概念以及它与源阻抗和负载阻抗的关系，也会研究元件的损耗，以及它们是如何影响电路的，最后将展示一些耦合谐振电路。

谐振电路应用在射频电路中每个发射器、接收器、测试设备上，选择性地将某个频率或一组频率从源传递到负载，同时衰减该通带之外的所有其他频率。理想的谐振电路是这样子的：

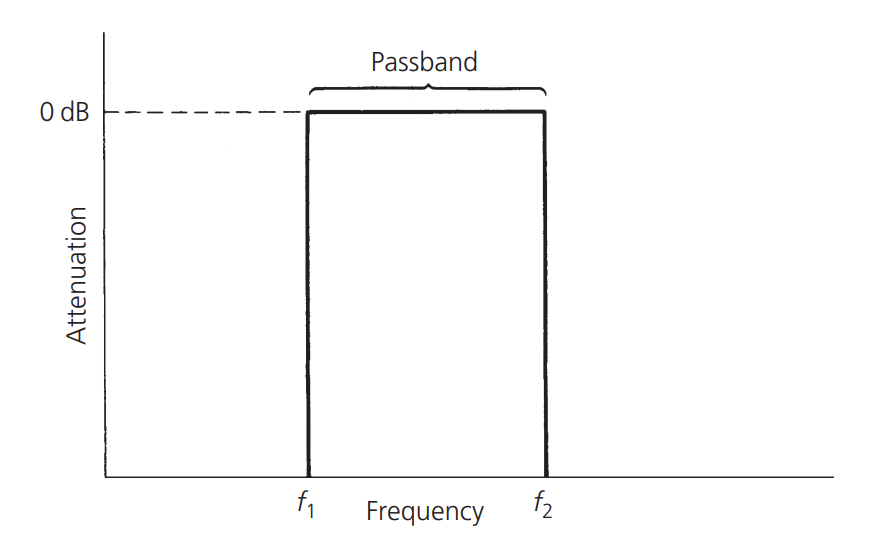
它是一个完美的矩形通带，在频率小于或大于目标带宽时无线衰减，同时允许目标贷款内的信号不受干扰地通过。但因为构成滤波器的元器件的物理属性，完美滤波器是不可能的，但我们可以设计满足需求的非理想滤波器。

带宽

带宽（Bandwidth）一般指半功率带宽，即幅值响应比带通响应低 3dB 处，上限频率与下限频率的差（$f_2-f_1$），如图所示：

dB 的含义与计算

dB 是个相对值，能够简短表示很大或很小的数。假如我们表示功率变化增大到 100000000 倍，只需要写 +80dB 即可。

$$dB=10\lg(\frac{P_1}{P_0})$$

其中，$P_1$ 表示当前功率，$P_0$ 表示参考功率。假如 $P_1$ 是 $P_0$ 的两倍，那么：

$$10\lg(\frac{P_1}{P_0})=10\lg2=3dB$$

假如 $P_1$ 是 $P_0$ 的一半，那么：

$$10\lg(\frac{P_1}{P_0})=10\lg\frac{1}{2}=10\lg2^{-1}=-3dB$$

同理，+10dB 表示功率增大 10 倍，-10dB 表示功率减小为 1/10。

3 dB 在功率图或误码率图中经常出现，指的是 +3 dB 表示增大为两倍，-3 dB 表示下降为 1/2。

dBm 与 dBw

dBm、dBw 就是把 dB 公式中的参考功率 P0 分别换成 1 mW、1 W：

$$dBm=10\lg(\frac{P_1}{1mW})$$

$$dBw=10\lg(\frac{P_1}{1W})$$

因为 1 mW、1 W 都是确定的值，因此 dBm、dBw 都可以表示功率的绝对值。

有一个当前功率与使用 dBm、dBw 的换算表：

watt	dBm	dBw
0.1 pW	-100 dBm	-130 dBW
1 pW	-90 dBm	-120 dBW
10 pW	-80 dBm	-110 dBW
100 pW	-70 dBm	-100 dBW
1 nW	-60 dBm	-90 dBW
10 nW	-50 dBm	-80 dBW
100 nW	-40 dBm	-70 dBW
1 μW	-30 dBm	-60 dBW
10 μW	-20 dBm	-50 dBW
100 μW	-10 dBm	-40 dBW
794 μW	-1 dBm	-31 dBW
1.000 mW	0 dBm	-30 dBW
1.259 mW	1 dBm	-29 dBW
10 mW	10 dBm	-20 dBW
100 mW	20 dBm	-10 dBW
1 W	30 dBm	0 dBW
10 W	40 dBm	10 dBW
100 W	50 dBm	20 dBW
1 kW	60 dBm	30 dBW
10 kW	70 dBm	40 dBW
100 kW	80 dBm	50 dBW
1 MW	90 dBm	60 dBW
10 MW	100 dBm	70 dBW

其中，最常用的是 1 W = 30 dBm。

dBi、dBd 与 dBc

dBi、dBd 与 dBc 的计算方法与 dB 相似，表示的是功率相对值，但参考基准 $P_0$ 所代表的含义不同。

dBx	参考基准
dBi（Decibe-Isotropic）	全方向性天线（Isotropic antenna）
dBd（Decibe-Dipole）	偶极子天线（Dipole antenna）
dBc（Decibe-Carrier）	载波（Carrier）

表示同一增益，dBi 一般比 dBd 大个 2.15，这个差值是两种天线的不同方向性导致的。

谐振电路的中心频率与其带宽之比（Q）

此 Q 与上一篇文章的 Q 定义不同。Q 是谐振电路选择性的量度，Q 值越高，带宽越窄，谐振电路的选择性就越高。Q 的公式定义如下：

$$Q=\frac{f_e}{f_2-f_1}$$

形状因子（Shape Factor, SF）

谐振电路的形状因数通常定义为谐振电路 60dB 带宽与 3dB 带宽之比。举个例子，如果 60dB 带宽 $f_4 - f_3$ 为 3 MHz，3dB 带宽 $f_2-f_1$ 为 1.5 MHz，则形状因子为：

$$SF=\frac{3MHz}{1.5MHz}=2$$

形状因子是衡量裙边陡峭程度的一种方式。数字越小，响应裙边越陡峭。完美滤波器的形状因子为 1，这是终极取值。形状因子比 1 小的通带如下图，但这在物理上是不可能的：

极限衰减（Ultimate attenuation）

指的是通带与带通外衰减峰值之差。受元器件实际物理特性影响，极限衰减不可能是无限的。

插入损耗（Insertion Loss）

指在信号源段与末端之间的组件造成的衰减损耗。在阻抗没有匹配的情况下，因为这些组件的阻性，源端有些信号会被这些组件吸收，这里造成的衰减就叫插入损耗，以 dB 表示。

纹波（Ripple）

纹波表示谐振电路通带的平坦度，以 dB 表示。它的值定义为通带中的最大衰减与最小衰减的差。

参考与致谢

• 《RF-Circuit-Design(second-edition)_Chris-Bowick》
• 100 分钟看懂 dB、dBm、dBw 的区别

本篇文章受 CC BY-NC-SA 4.0 协议保护，转载请注明出处。