Skip to main content

数字电路基础知识

数制与码制​

数制：表示数量的规则。每一位的构成、从低位向高位的进位规则，例如十进制。 码制：表示事物的规则，编码时遵循的规则。

模拟电路：用连续的模拟电压 / 电流值来表示信息 数字电路：用一个离散的电压序列来表示信息

常用到的进制：

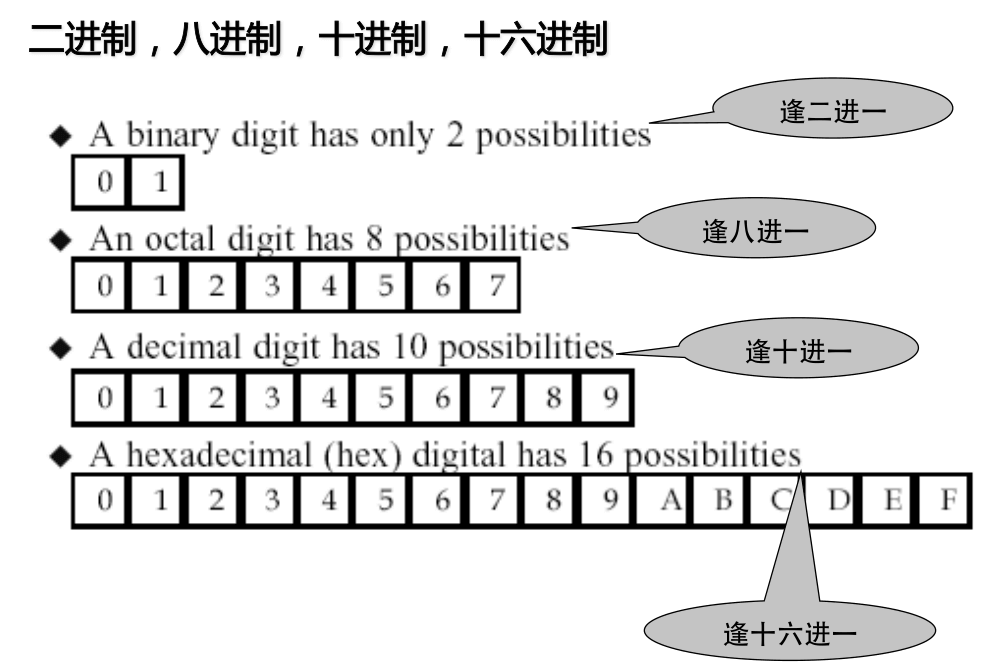
任意进制的数转为十进制：

(526)8=5∗82+2∗81+6∗80=(342)10(526)_8=5*8^2+2*8^1+6*8^0=(342)_{10}

(2A.7F)H=2∗161+10∗160+7∗16−1+15∗16−2=(42.4960937)D(2A.7F)_H=2*16^1+10*16^0+7*16^{-1}+15*16^{-2}=(42.4960937)_D

D=∑KiNiD=\sum K_iN^i

二进制的补码​

  • 最⾼高位为符号位（0 为正，1 为负）
  • 正数的补码和它的原码相同
  • 负数的补码 = 数值位逐位求反 + 1

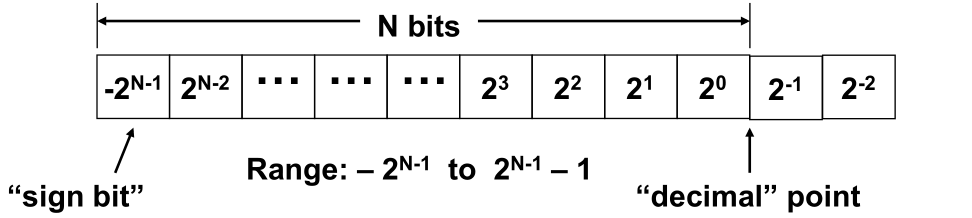
+5 = （0 0101）
-5 = （1 1011）

1101.0110
= –2 3 + 2 2 + 2 0 + 2 -2 + 2 -3
= – 8 + 4 + 1 + 0.25 + 0.125
= – 2.625

码制​

等长编码：

  • 4 位 BCD 码
  • ASCII
  • 格雷码：编码顺序依次变化，按表中顺序变化时，相邻代码只有⼀一位改变状态

逻辑代数基础​

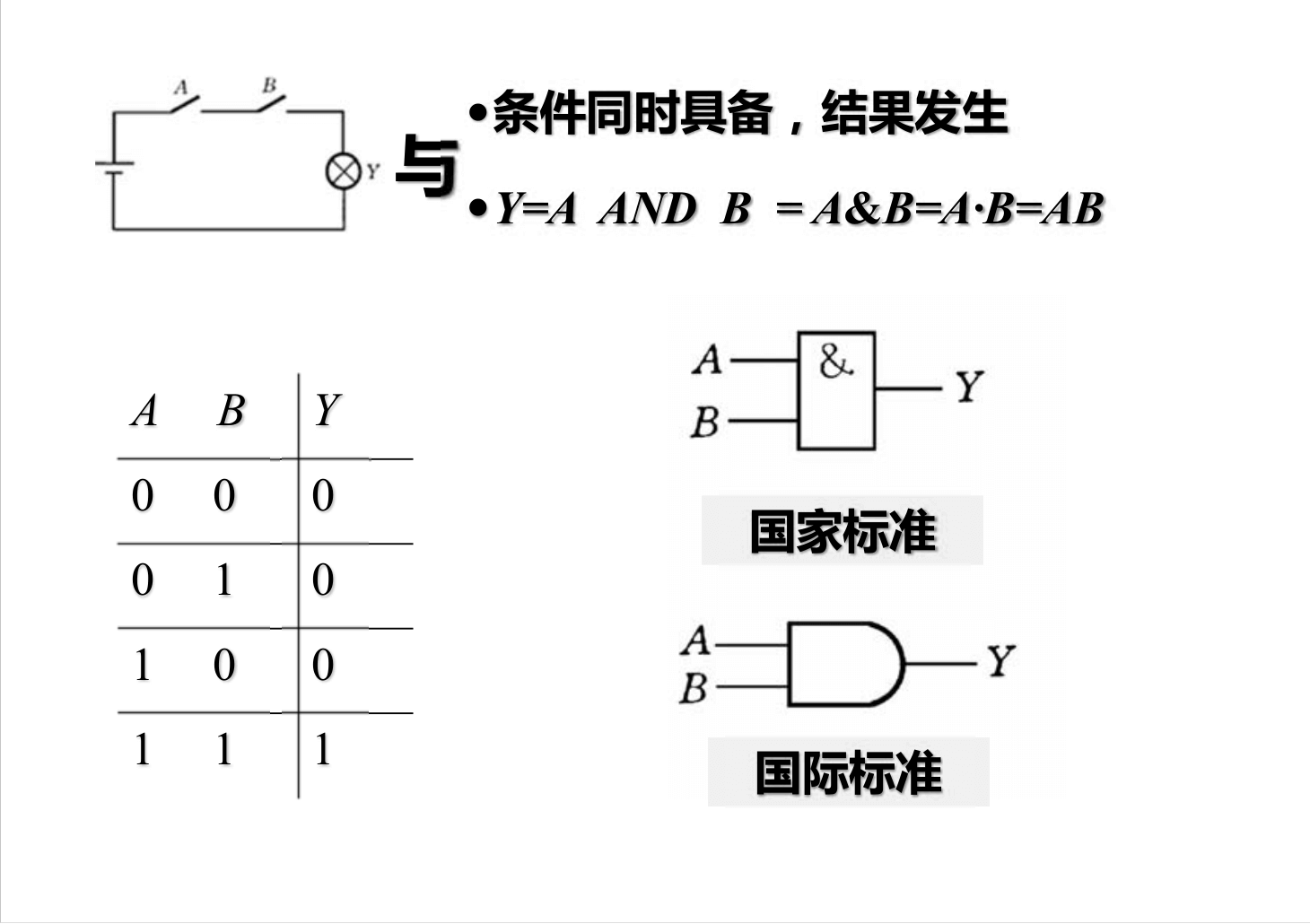
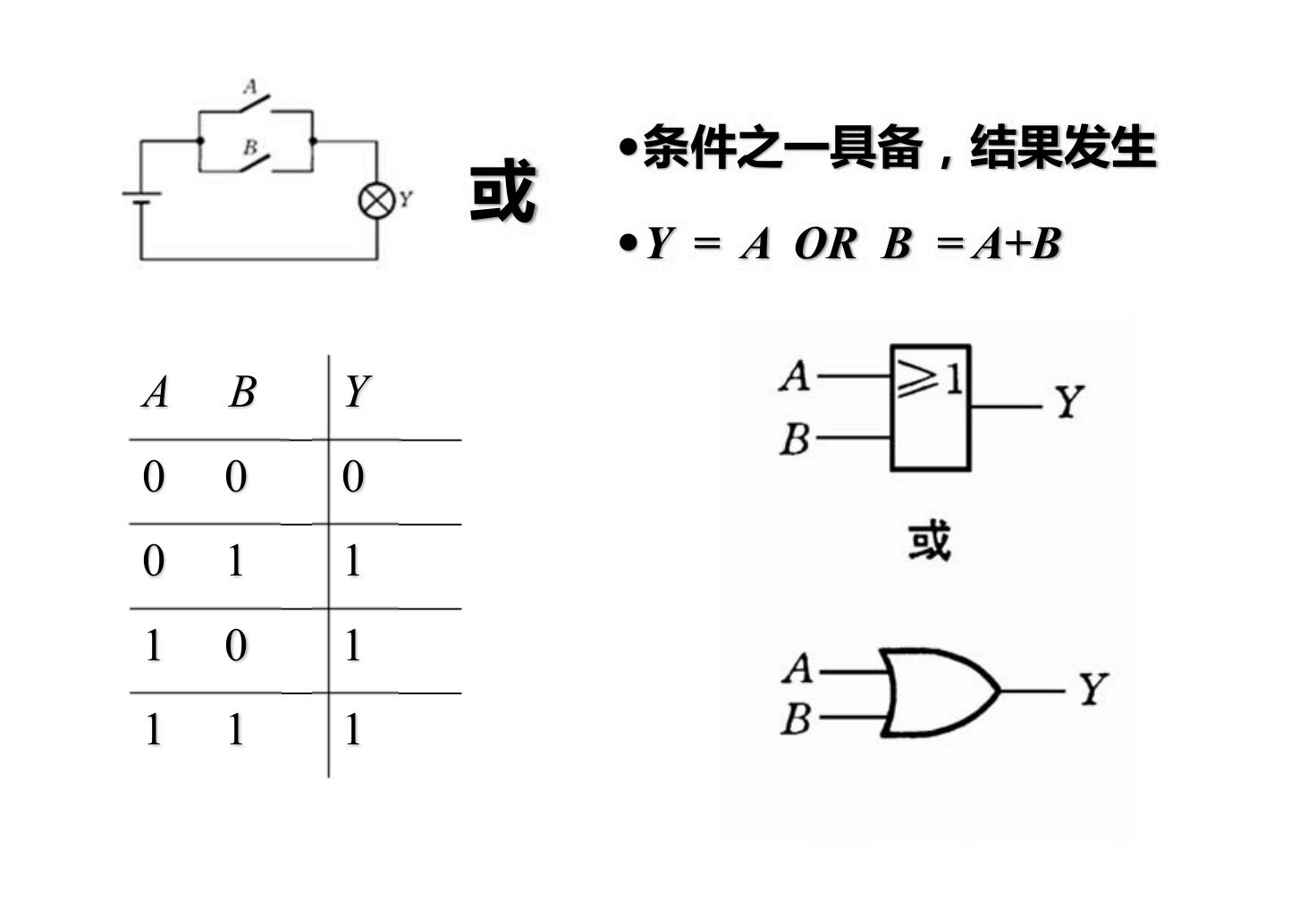
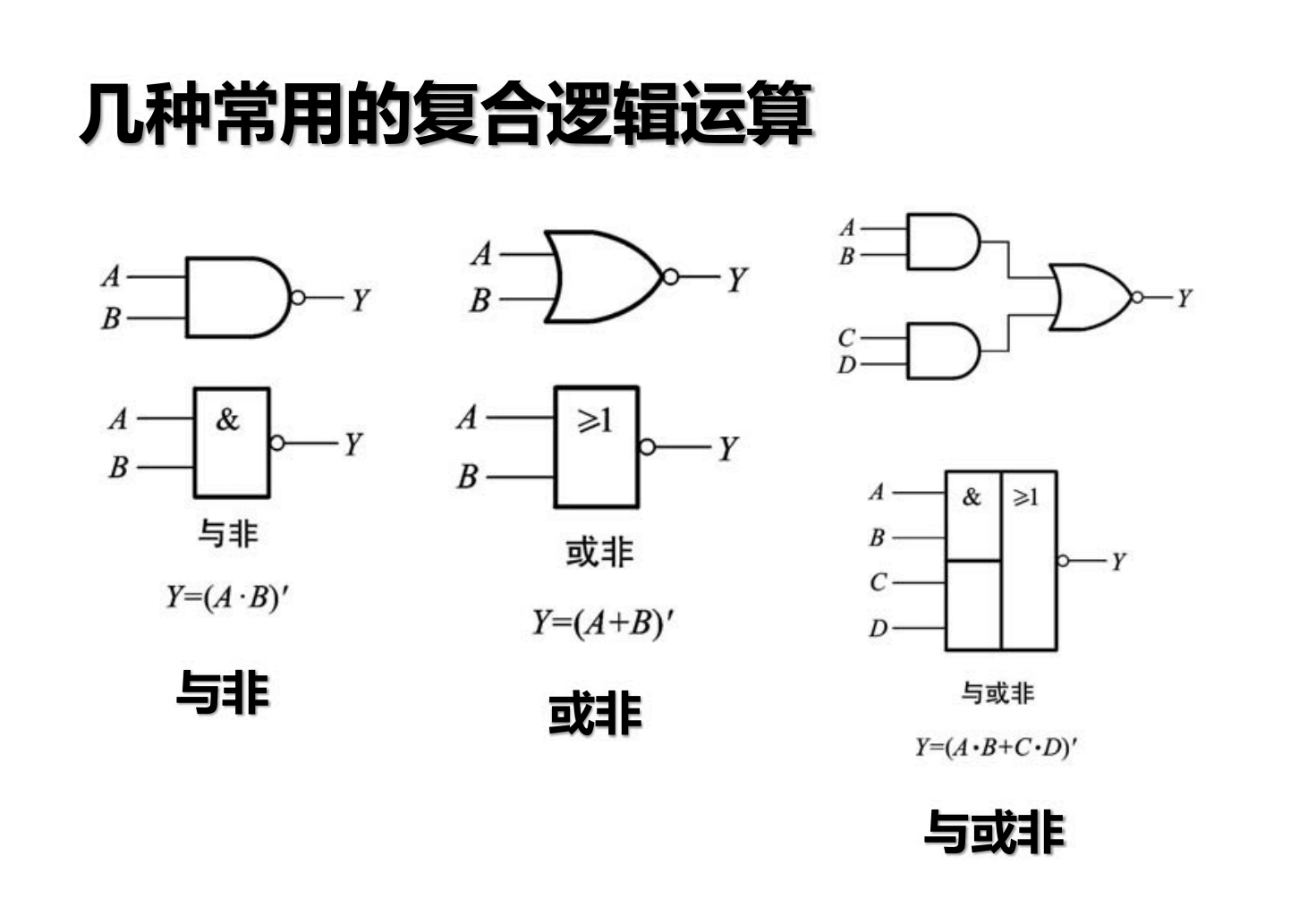
异或：不同为 1，相同为 0
Y=A′B+AB′Y=A'B+AB'

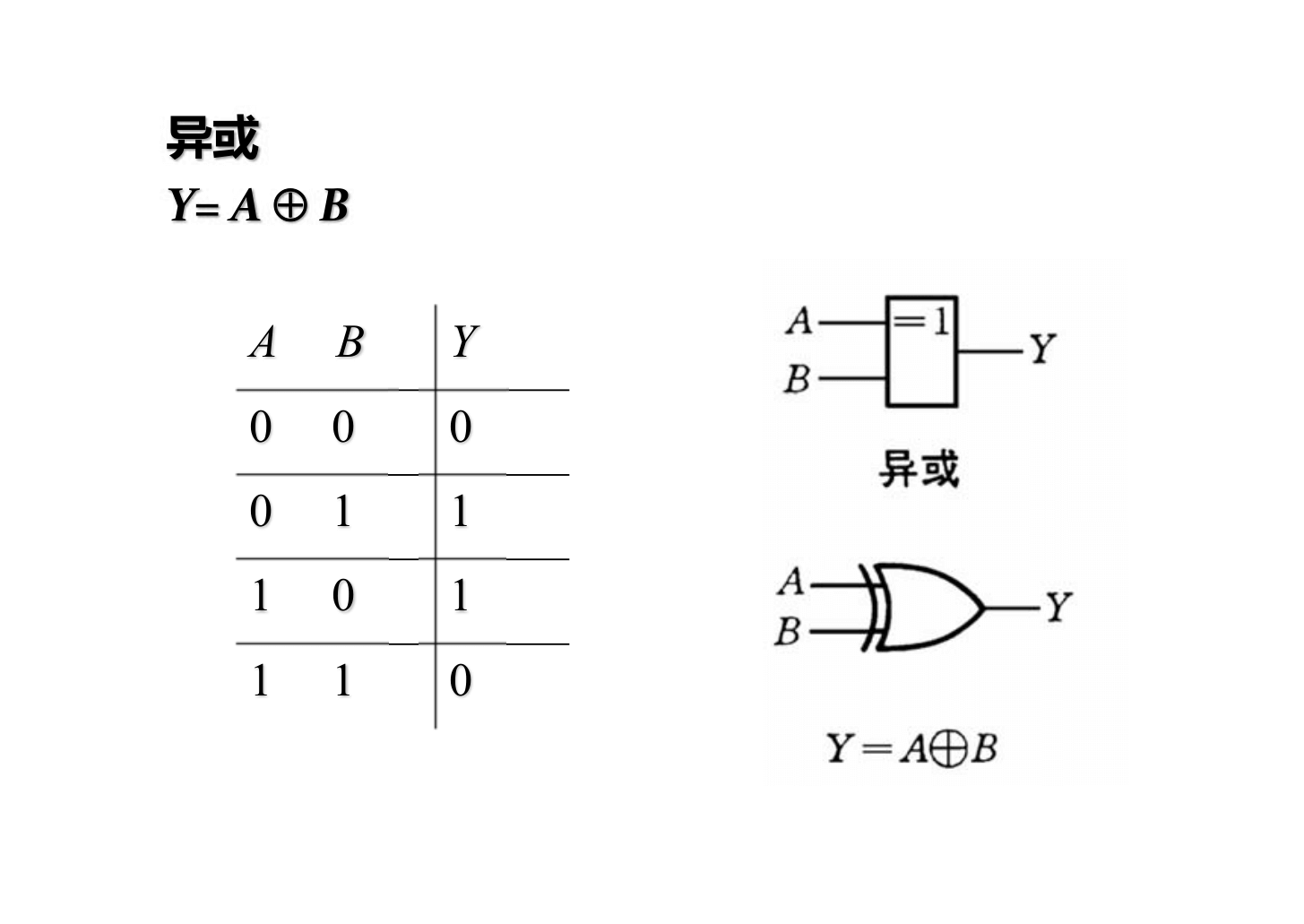
同或：相同为 1，不同为 0 Y=AB+A′B′Y=AB+A'B'

逻辑运算基本公式​

(AB)′=A′+B′(A B) ' = A' + B'
(A+B)′=A′B′(A+ B)' = A'B'
A+BC=(A+B)(A+C)A + B C = (A +B)(A +C)

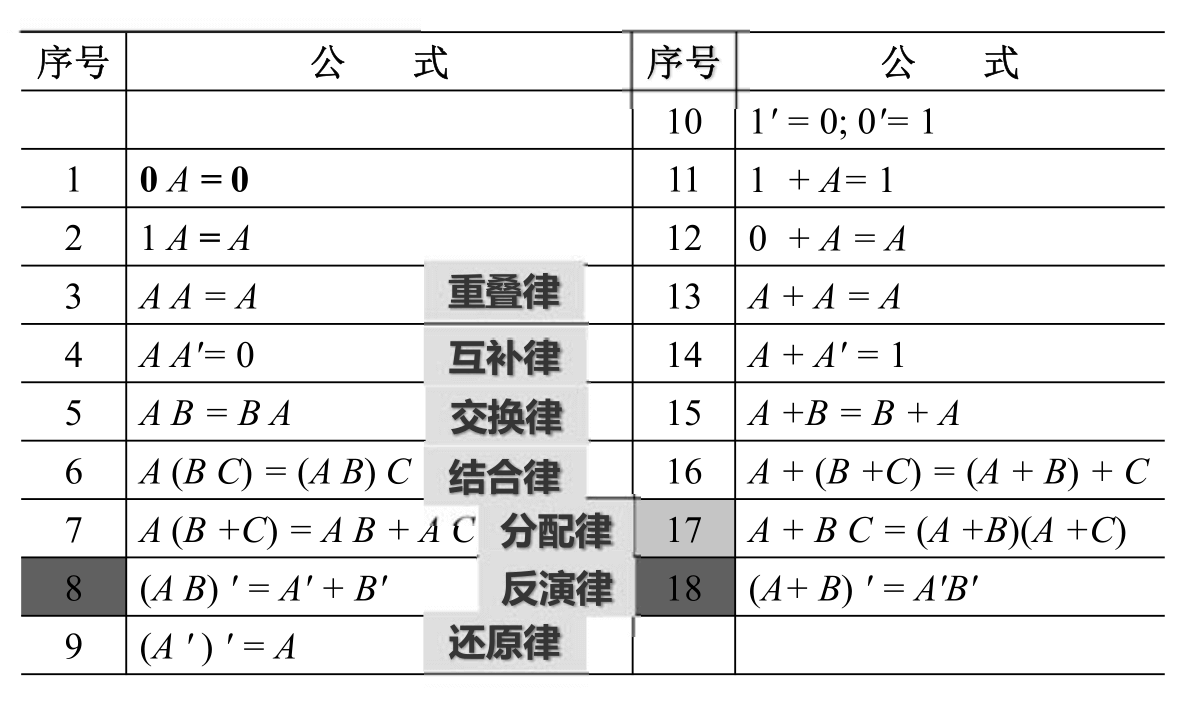
逻辑运算常用公式​

逻辑代数基本定理​

逻辑函数的表示方法​

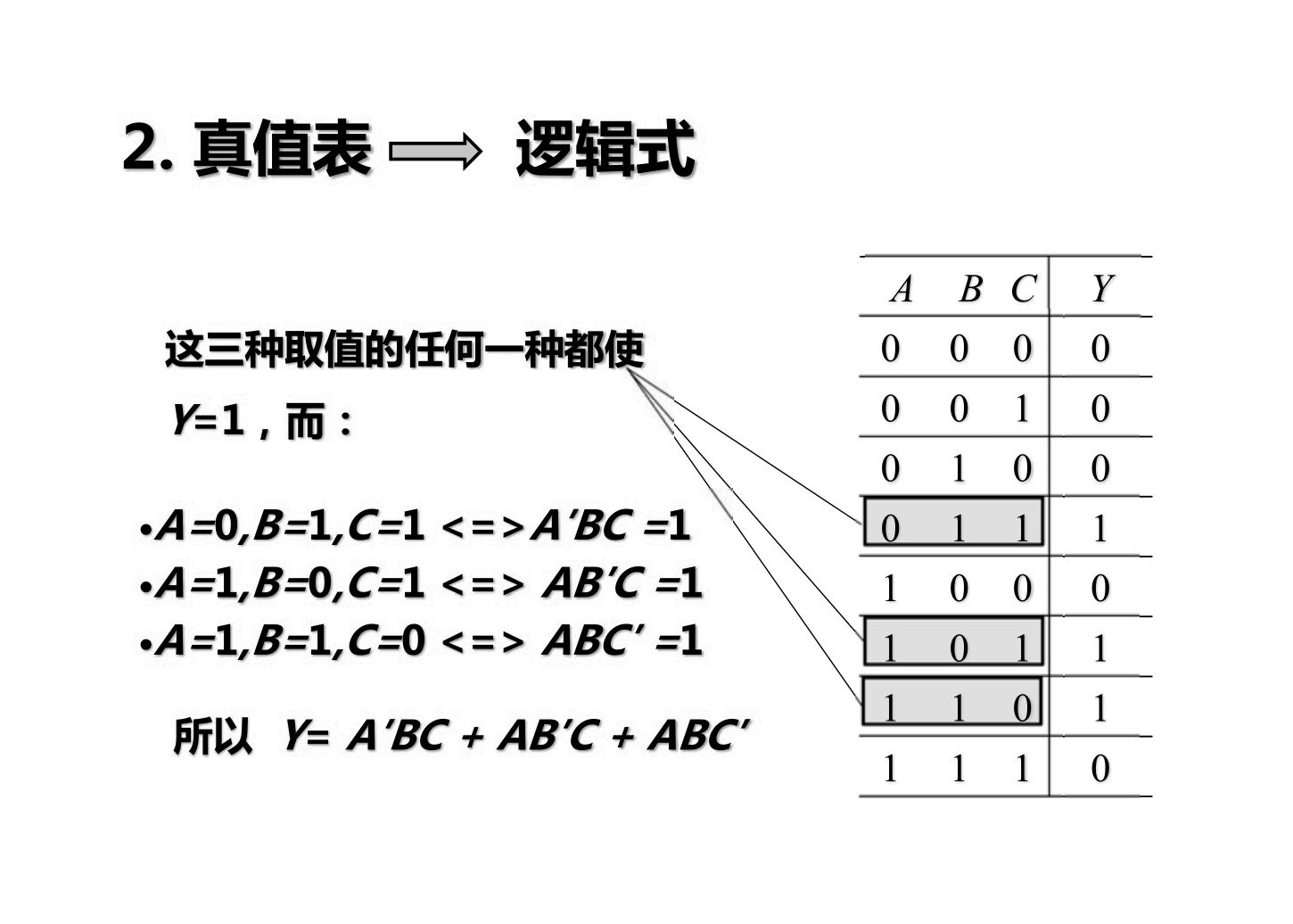
  • 真值表
  • 逻辑式
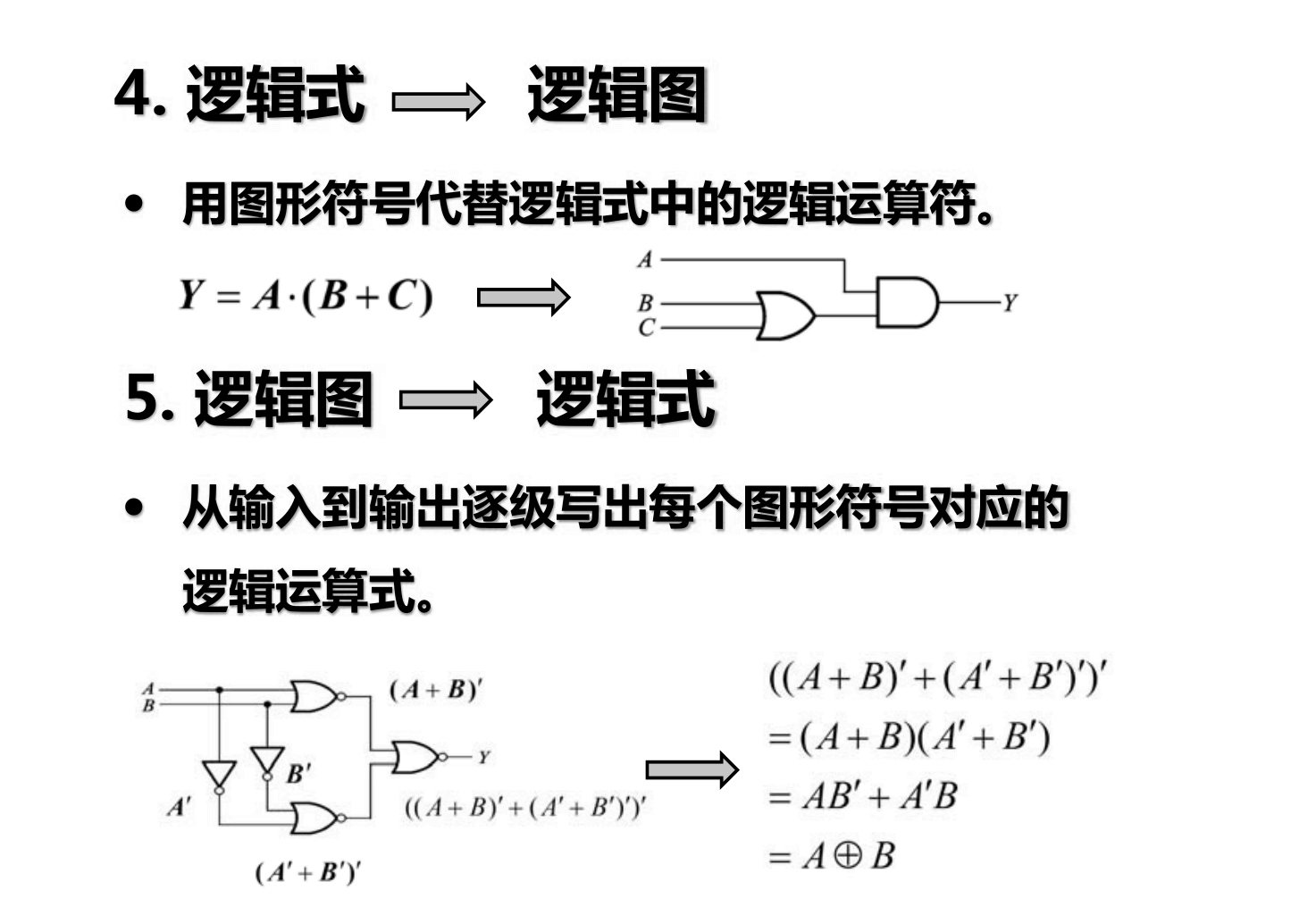
  • 逻辑图
  • 波形图

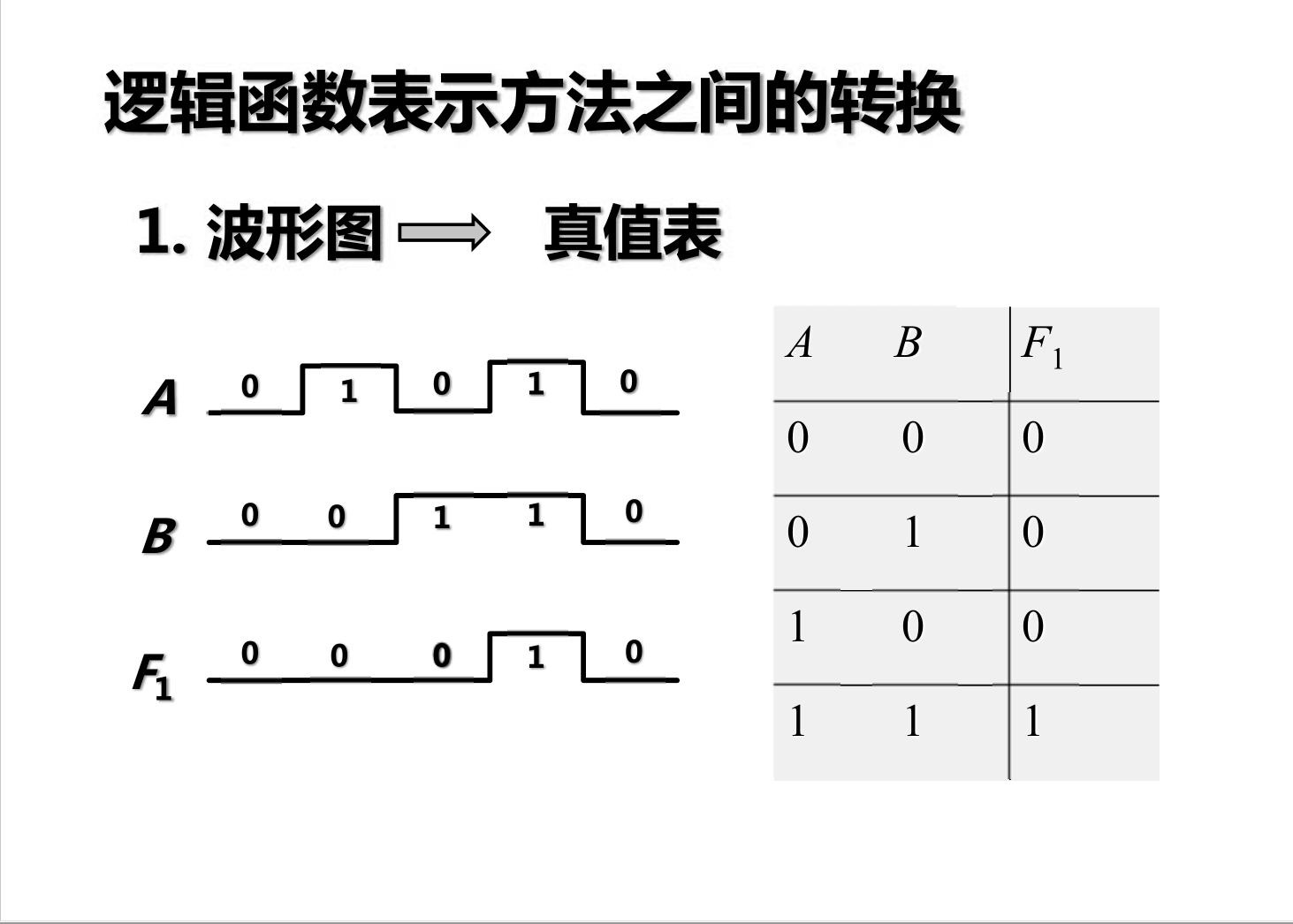
逻辑函数的公式化简法​

逻辑式的最简形式​

最小项

其实就是真值表中的行数
代表所有可能、唯一的情况

公式化简法​

反复应用基本公式和常用公式，消去多余的与项和 多余的因子。

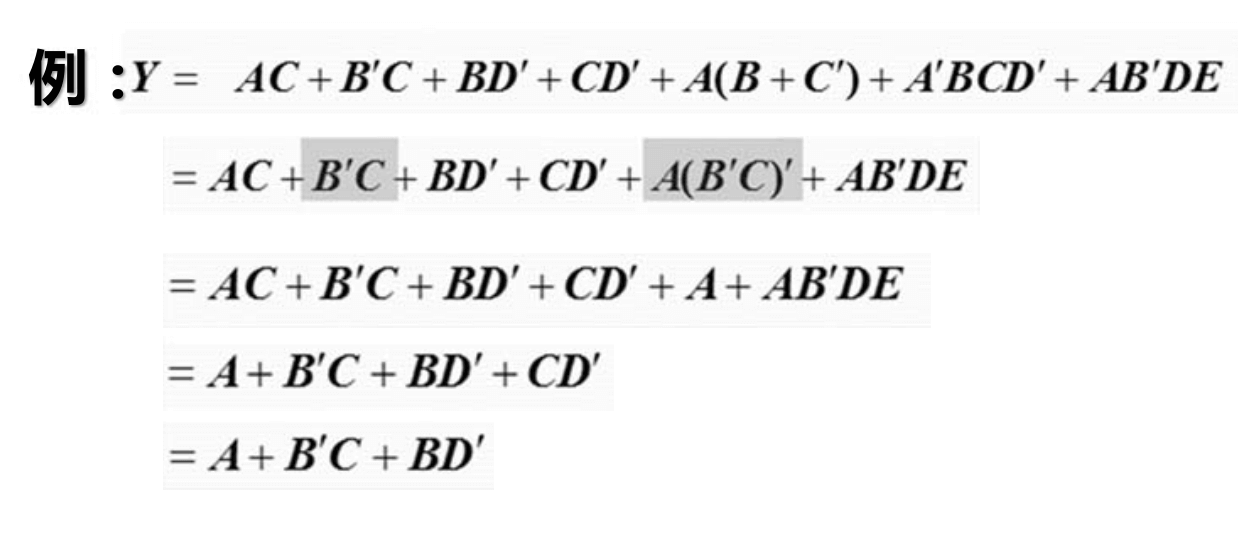
卡诺图化简法​

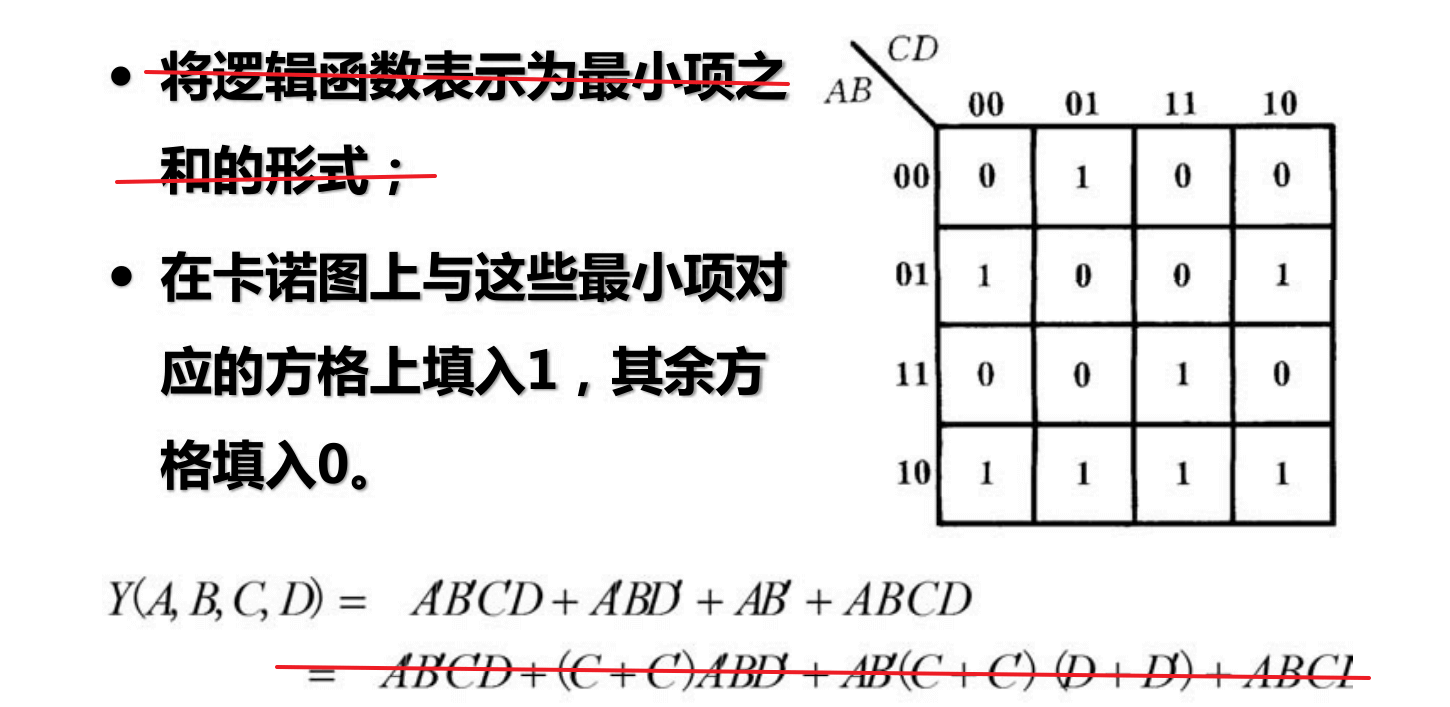
不必全化为最小项。
如果最小项重复，则填 1.

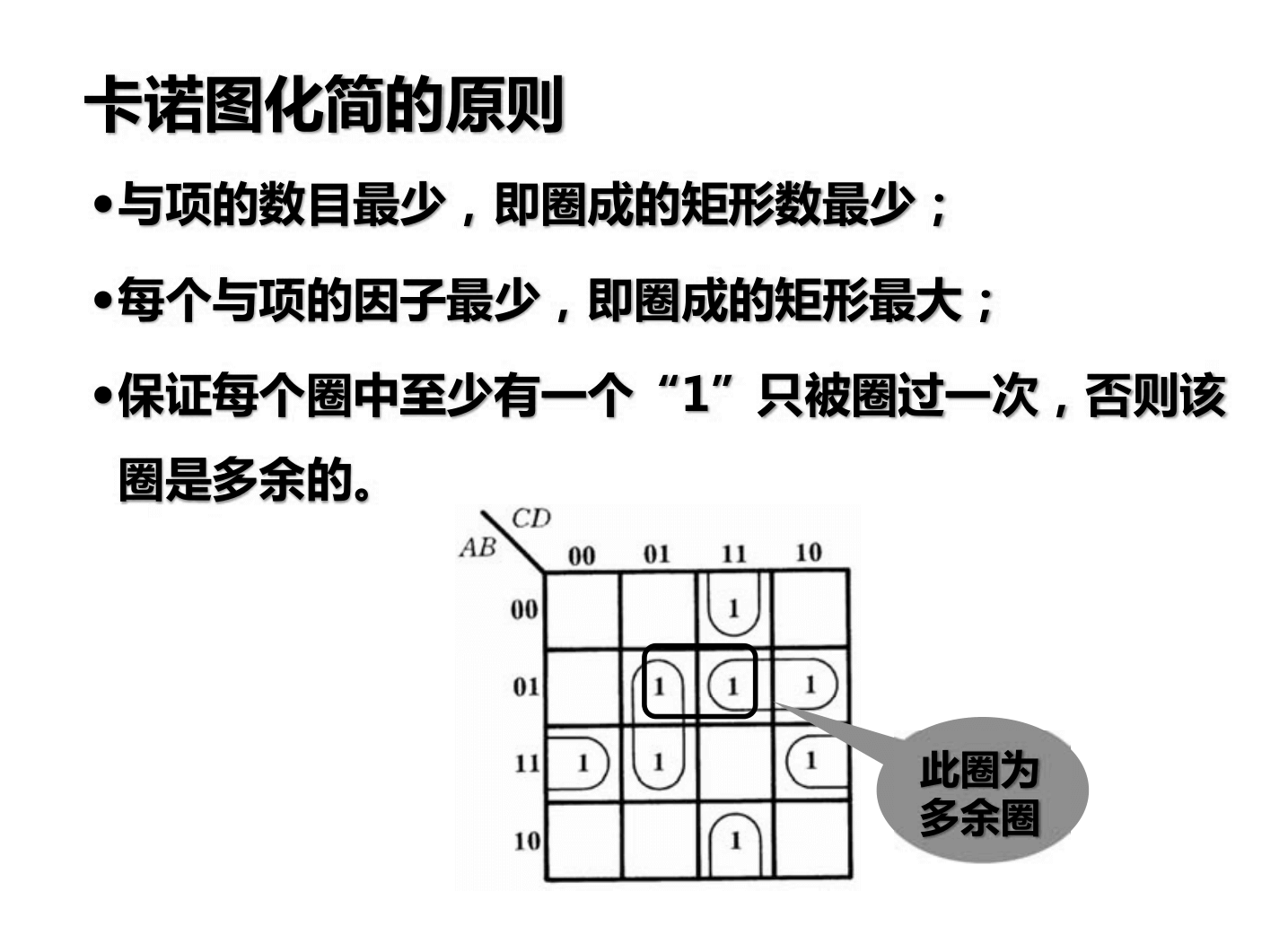
如果 0 比较少，也可以圈 0 后取反。

门电路​

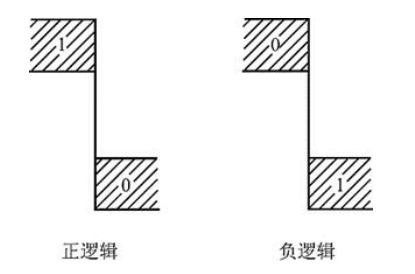
正逻辑与负逻辑​

如果以高电平表示逻辑 1，以低电平表示逻辑 0，则称这种表示方法为正逻辑；反之，则称这种表示方法为负逻辑。

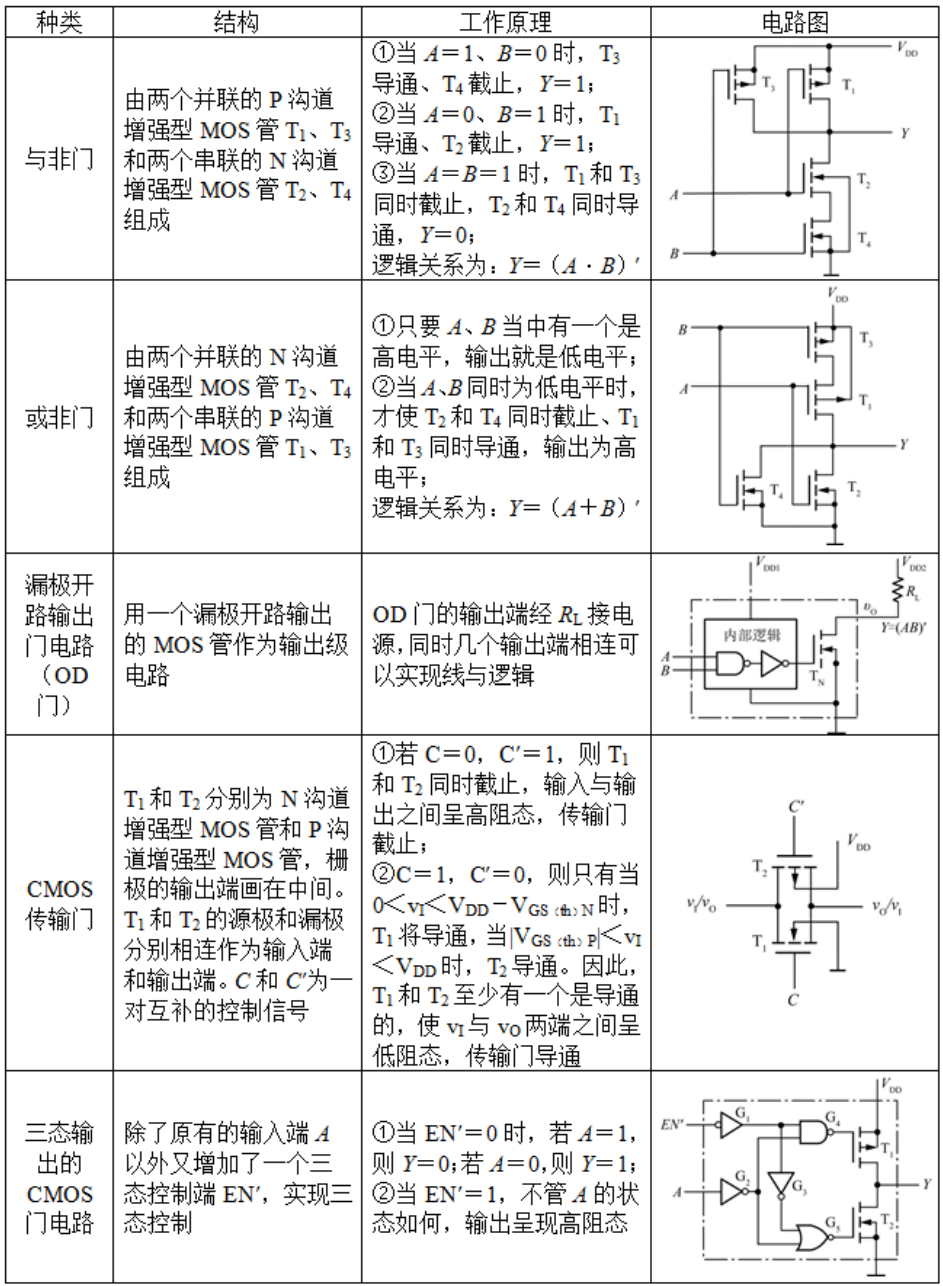
CMOS 管门电路​

参考与致谢​

  • 《编码：隐匿在计算机软硬件背后的语言》

本篇文章受 CC BY-NC-SA 4.0 协议保护，转载请注明出处。